Suite de la série sur les lentilles
Publié le 09 décembre 2015
Où l'on finira par conjuguer puis par diverger.
Introduction à la loi des lentilles
Pour un montage optique d’imagerie à une lentille nous établissons le lien qui existe entre la distance « objet » (qui sépare l’objet de la lentille) et la distance « image » (qui sépare l’image de la lentille). Nous faisons cela à l’aide de l’analyse géométrique du tracé de deux rayons particuliers passant au travers de la lentille : le rayon qui est initialement parallèle à l’axe optique de la lentille et le rayon qui passe par le centre de la lentille. Une étude des triangles semblables apparaissant dans ces tracés, permet effectivement d’obtenir une relation entre la distance « objet », la distance « image » et la distance focale de la lentille. Cette relation s’appelle la loi des lentilles. Elle permet de prédéterminer la distance « image » sur base de la connaissance de la distance « objet » et de la distance focale de la lentille. Nous illustrons la loi des lentilles à l’aide de plusieurs exemples pratiques qui démontrent sa cohérence par rapport à l’obtention de l’image par construction géométrique. Une de ces illustrations toutefois révèle la difficulté rencontrée lorsque la distance « objet » est inférieure à la distance focale de la lentille. Dans ce cas en effet, la loi des lentilles fournit une distance « image » négative, ce à quoi il est difficile de donner un sens (la distance entre deux points étant par définition une grandeur positive). Ce résultat motive la séquence suivante consacrée à une forme plus rigoureuse et plus complète de la loi des lentilles.
La relation de conjugaison des lentilles
Le point de départ de cette séquence est la loi des lentilles telle qu’obtenue par analyse géométrique dans la séquence précédente. Nous retraçons brièvement les difficultés rencontrées avec cette loi : distances négatives et besoin de deux lois de formes différentes pour des conditions différentes d’utilisation de la lentille (formation d’une image réelle ou formation d’une image virtuelle). Nous montrons que ces difficultés sont naturellement contournées à l’aide de l’utilisation de coordonnées de position en lieu et place des distances (distance « objet », distance « image » et « distance » focale). Nous introduisons ainsi dans la description des lentilles la notion de système de coordonnées cartésiennes telle que proposé par René Descartes lui-même au 17ème siècle. Nous sommes ainsi amenés à généraliser la loi des lentilles en l’exprimant sous la forme de la « relation de conjugaison » de René Descartes. Nous montrons à l’aide de plusieurs exemples que cette nouvelle forme de la loi des lentilles est cohérente et valable pour toutes les situations (notamment pour le cas de la formation d’images virtuelles).
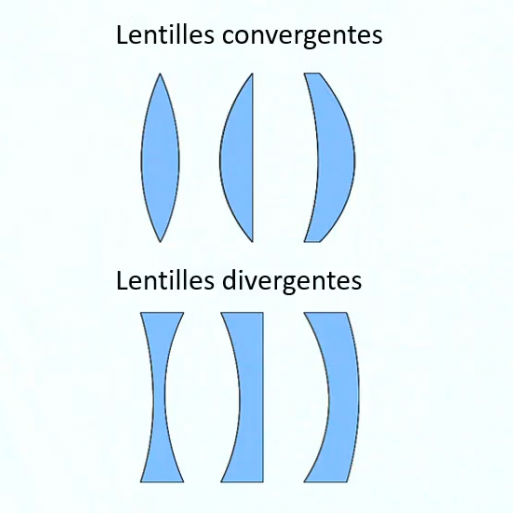
Nous introduisons les lentilles divergentes sur base d’un rappel de la physique de base des lentilles minces convergentes. Le parallèle ainsi établi entre les deux types de lentilles nous permet d’introduire la notion de foyer image « virtuel » qui caractérise les lentilles divergentes. La notion de foyer et de plan focal nous permet de procéder à la construction géométrique de l’image virtuelle formée par une lentille divergente. Nous montrons ensuite que la loi de conjugaison de Descartes est valable pour les lentilles divergentes à la condition qu’on leur associe une distance focale négative. Trois situations distinctes sont considérées pour illustrer la cohérence de la loi de conjugaison.

