La tangente : introduction

La fonction tangente est présentée au travers du calcul de la longueur du côté « opposé » du triangle rectangle sur base de la connaissance du côté « adjacent » et de l’angle correspondant. Ce calcul est fait dans le contexte d’un problème de géométrie concret qui consiste en la mesure de la hauteur d’un bâtiment. Cette façon de procéder permet d’introduire naturellement la fonction tangente comme étant le rapport des fonction sinus et cosinus. L’utilité de la fonction tangente est illustrée au travers d’une problématique de calcul de pente pour les besoins d’un saut en « wingsuit ». Le lien important existant entre la notion de pente (au sens mathématique du terme) et la fonction tangente est ainsi clairement établi.

La fonction tangente

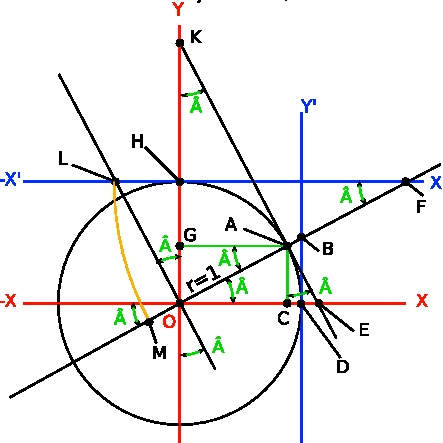
A partir de la représentation de la tangente sur le cercle trigonométrique, nous procédons à l’étude de la tangente en tant que fonction mathématique. En particulier, nous en construisons le graphe en considérant un angle variant progressivement entre 0° et 360°. Nous montrons que la tangente d’un petit angle (angle en radian très inférieur à l’unité) est à peu près égal à cet angle lui-même lorsque ce dernier est exprimé en radian. Nous passons ensuite à la tangente des angles remarquables 0°, 30°, 45°, 60° et 90°. Nous insistons plus particulièrement sur le comportement asymptotique de la tangente autour des angles 90° et 270°. Nous insistons également sur la périodicité de la fonction tangente (période π) qui permet d’en calculer la valeur pour des angles des 2ème, 3ème et 4ème quadrant à partir de sa connaissance pour des angles du premier quadrant. Enfin nous soulignons la nature antisymétrique (impaire) de la fonction tangente. Une très brève discussion de la différence entre pente (tangente) et déclivité (sinus) est donnée en guise d’illustration.