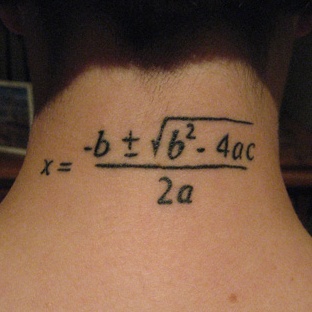
L’équation du second degré : résolution algébrique

Le calcul des solutions de l’équation algébrique du second degré est fait de manière progressive à partir de la construction de l’équation sous sa forme canonique. Cette forme de l’équation a le double avantage de permettre un calcul simple des solutions et d’en faciliter l’interprétation. La notion de discriminant est introduite et brièvement discutée en termes de conditions d’existence des solutions.

L’équation du second degré : interprétation géométrique

Cette séquence fait suite à la vidéo consacrée au calcul des solutions de l’équation algébrique du second degré. Nous y proposons l’interprétation géométrique des développements algébriques basés sur la construction progressive de la forme canonique de l’équation. Pour cela nous proposons l’analyse des graphes associés aux polynômes rencontrés dans ces développements. Les solutions de l’équation sont naturellement vues comme les intersections des paraboles correspondantes avec l’axe des abscisses. Ceci permet d’interpréter la formule donnant les solutions de l’équation en relation avec la valeur du discriminant (conditions d’existence des solutions).

L’équation du second degré : illustration

Un problème pratique lié à une trajectoire balistique est proposé pour illustrer la formule donnant les solutions de l’équation algébrique du second degré. D’une part nous proposons de calculer le point de chute d’un tir balistique ; il s’agit dans ce cas d’appliquer simplement la formule et d’éliminer une des deux solutions fournies par interprétation physique. D’autre part nous proposons de déterminer la hauteur maximale atteinte sur trajectoire. La résolution de ce problème, beaucoup plus ardu, exige le recours à l’interprétation géométrique de la formule telle que proposée dans la vidéo précédente consacrée à ce thème. Notre principale motivation dans cette séquence est de démontrer que l’interprétation de la formule donnant les solutions de l’équation du second degré est indispensable à la résolution de certains problèmes concrets impliquant des polynômes du second degré.