Les nombres imaginaires

Nous commençons cette vidéo en rappelant la règle de l’arithmétique qui dit que le produit de deux nombres négatifs donne un nombre positif (la règle que l’on résume par la petite phrase « moins par moins donne plus »). Nous passons ensuite à la notion mathématique de racine carrée que nous définissons de façon formelle. Sur base de cette définition, nous montrons que la règle « moins par moins donne plus » interdit l’existence de la racine carrée de nombres réels négatifs. Nous introduisons alors les nombres imaginaires comme étant les nombres qui brisent cet interdit, c’est à dire, les nombres résultant de l’application de la définition de la racine aux nombres négatifs. Nous proposons une perspective historique en citant les travaux de Cardan du 16ème siècle. De même, nous présentons brièvement plusieurs applications de physique moderne du nombre « i » (défini comme la racine carrée de « -1 »), de façon à en comprendre l’importance pratique. Nous concluons la séquence par quelques petits exercices en guise de préparation à la découverte des nombres complexes.

Les nombres complexes

Sur base de la connaissance acquise dans la séquence sur les nombres imaginaires, les nombres complexes sont introduits comme les nombres formés de la somme d’un nombre réel et d’un nombre imaginaire. Les opérations élémentaires d’addition et de multiplication sont présentées. Nous insistons sur la simplicité des règles de calculs qui sont fondamentalement les mêmes que celles appliquées aux nombres réels. Les notions de nombre complexe « conjugué » et de « module » sont introduites très brièvement.

Division des nombres complexes

Après un bref rappel de la notion de nombre complexe, nous présentons, sous forme d’un exercice, une procédure permettant le calcul du quotient de deux nombres complexes. Ensuite nous montrons que le même résultat peut-être obtenu beaucoup plus simplement en exploitant la notion de nombre complexe conjugué. Sur cette base nous établissons la formule donnant l’inverse d’un nombre complexe, ce qui permet de calculer le quotient de nombres complexes quelconques.

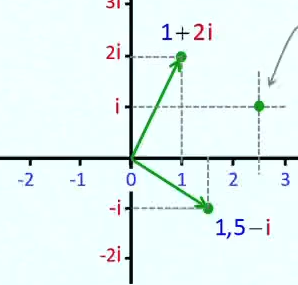
Représentation géométrique des nombres complexes

Sur base du parallèle évident existant entre la règle d’addition des nombres complexes et la règle d’addition des vecteurs, nous introduisons la représentation géométrique des nombres complexes. Dans cette perspective, les parties réelle et imaginaire d’un nombre complexe apparaissent comme l’analogue des composantes d’un vecteur dans le plan. En particulier le module du nombre complexe apparaît clairement dans cette analogie comme l’équivalent de la norme d’un vecteur.

Nous illustrons la représentation géométrique des nombres complexes en interprétant géométriquement la règle d’addition des nombres complexes, ainsi qu’au travers de la représentation de l’opposé et du conjugué d’un nombre complexe. 

Forme polaire des nombres complexes

Un bref rappel de la représentation géométrique des nombres complexes nous conduit à insister sur le parallèle que cette représentation permet d’établir entre les nombres complexes et les vecteurs, en particulier, en ce qui concerne la loi d’addition. Une fois ce parallèle clarifié nous introduisons la forme polaire des nombres complexes au travers de la notion de coordonnées polaires : un vecteur représentant une position dans le plan peut être déterminé de façon univoque par l’angle que fait ce vecteur avec l’axe des abscisses et sa norme (distance du point à l’origine des axes). Le nombre complexe est alors exprimé en termes de module et d’argument. Nous discutons ensuite de la conversion entre la forme cartésienne et la forme polaire des nombres complexes. Au travers d’un exemple, nous attirons l’attention de l’élève sur l’indétermination inhérente à la fonction arc-tangente nécessaire à cette conversion.

Produits et puissances de nombres complexes

Après avoir montré que la forme cartésienne des nombres complexes n’est pas adaptée à l’interprétation géométrique du produit de deux nombres complexes, nous effectuons le calcul de ce produit à l’aide de la forme polaire des nombres complexes. Ce calcul nous mène aux expressions des sinus et cosinus d’une somme d’angles. Nous arrivons ainsi à la conclusion que le nombre complexe « produit » a pour argument la somme des arguments des deux facteurs du produit. Ce résultat est ensuite appliqué au calcul de puissances de nombres complexes, ce qui nous permet d’établir la formule qui exprime que la mise à la puissance entière « n » d’un nombre complexe « z », conduit à un nombre complexe dont l’argument vaut « n » fois l’argument de « z » et dont le module vaut le module de « z » à la puissance « n ».

Tous les résultats obtenus sont illustrés à l’aide d’exemples simples.

Puissances négatives de nombres complexes

A partir de l’expression théorique de la puissance entière positive d’un nombre complexe, nous commençons par établir la formule de Moivre. La formule de Moivre est effectivement obtenue très simplement à partir de l’application de cette formule à un nombre complexe de module unitaire. Cette formule nous permet de calculer simplement l’expression d’un nombre complexe élevé à une puissance négative « -n » (où « n » est un entier positif). Après une brève discussion des propriétés des fonctions sinus et cosinus, nous arrivons à la conclusion que la formule donnant la puissance d’un nombre complexe peut être généralisée à des exposants négatifs (entiers).

Racines des nombres complexes

A partir de la formule donnant la puissance « n » d’un nombre complexe « z », nous établissons la formule donnant la racine d’ordre « n » d’un nombre complexe. En traitant le problème de façon volontairement simpliste pour commencer, nous arrivons à la conclusion que l’argument de la racine « n »-ème d’un nombre complexe « z » a pour valeur un « n »-ème de l’argument de « z ». Mais au travers de divers exemples simples nous montrons que, bien que correct, ce résultat n’est pas complet. Les exemples traités montrent effectivement que pour obtenir toutes les valeurs possibles de la racine « n »-ème d’un nombre complexe, il faut adresser le problème l’ambiguïté de la définition de l’argument d’un nombre complexe. En effet, l’argument d’un nombre complexe a une valeur déterminée à un multiple de 360° près et c’est bien en tenant compte de cette indétermination que l’on arrive à considérer toutes les racines d’un nombre complexe. Nous montrons de cette façon que les racines « n »-ème d’un nombre complexe sont au nombre de « n » et que, dans le plan complexe, elles se situent toutes, à intervalle régulier, sur le même cercle centré sur l’origine.