6 vidéos ayant le tag “produit matriciel”
-
Mathématiques
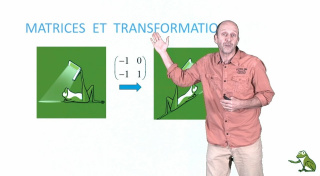
Matrices et transformations
Les transformations dans le plan sont exploitées pour illustrer et interpréter les propriétés du calcul matriciel. Dans cette perspective nous discutons les notions de matrice inverse, de racine carrée d’une matrice, de produit matriciel ainsi que de déterminant.
-
Mathématiques
Le calcul matriciel : 4. La matrice identité
Sur base de la formule de l’inverse d’une matrice (2x2) nous montrons que le produit d’une matrice avec son inverse donne la matrice identité (2x2). Nous montrons que cette matrice constitue l’élément neutre de l’opération de multiplication matricielle. A l’aide de la formule du produit de deux matrices de dimensions quelconques, nous généralisons le concept de matrice identité à l’ordre (nxn).
-
Mathématiques
Le calcul matriciel : 3. propriétés de la multiplication
L’objectif de cette séquence est de démontrer les propriétés de base du produit matriciel : la non-commutativité, la distributivité (par rapport à la loi d’addition des matrices) ainsi que l’associativité. La connaissance de ces démonstrations n’est pas indispensable à la maîtrise du calcul matriciel mais cette séquence est malgré tout conseillée car elle permet de se familiariser avec le formalisme matriciel.
-
Mathématiques
Le calcul matriciel : 2. La multiplication
L’objectif de cette séquence est de généraliser la rège du produit matriciel au cas de matrices d’ordre (mxn) quelconque. La règle est formulée sur base de la notation indicielle compacte des matrices. La condition à respecter sur les ordres (dimensions) des matrices est établie.
-
Mathématiques
Le calcul matriciel : 1. L’addition
Nous présentons et analysons la loi d’addition pour les matrices, en particulier, nous passons en revue ses propriétés de distributivité, associativité et commutativité.
-
Mathématiques
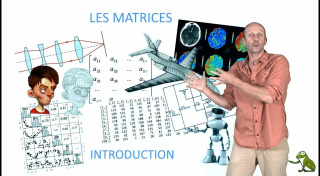
Les Matrices : introduction
Le concept mathématique de matrice est introduit dans le contexte de la résolution d’un système de deux équations linéaires à deux inconnues. L’internaute est amené à découvrir la notation des matrices, le produit matriciel (entre une matrice carrée et une matrice colonne), la notion de déterminant, de matrice inverse et la multiplication d’une matrice par un scalaire.
