122 résultats pour “co”
-
Physique
La loi d’Ohm, la résistance électrique
Nous expliquons l’origine physique de la loi d’Ohm sur base des notions de potentiel électrique et de courant électrique. L’approche consiste à calculer l’expression du courant électrique dans un matériau conducteur sur base de la notion de mobilité électronique.
-
Physique
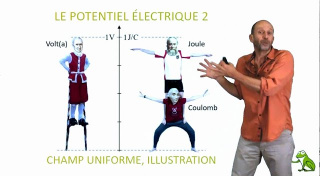
Le potentiel électrique 2 : champ uniforme, illustration
L’objectif de cette séquence est de montrer que la notion de potentiel électrique peut, au travers de considérations énergétiques, être exploitée pour décrire le comportement des charges électriques.
-
Physique
Méthode de Gauss 3 : le plan
Nous appliquons la loi de Gauss au calcul du champ électrique généré par une plaque rectangulaire uniformément chargée, y compris en des points intérieurs à la plaque elle-même.
-
Physique
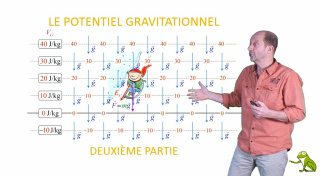
Le potentiel : introduction II
Nous généralisons la notion de potentiel gravitationnel vue dans la première partie au cas d’un champ d’accélération gravitationnelle en 1/r2 (cf. loi de la gravitation universelle), ceci dans le but de préparer l’élève au potentiel électrique de la charge ponctuelle (potentiel coulombien).
-
Physique
Le potentiel : introduction I
Dans le but de préparer l’élève au concept de potentiel électrique, nous introduisons la notion de potentiel dans le contexte de la force gravitationnelle. Dans cette première partie nous ne considérons que des situations à petite échelle à la surface de la Terre de sorte à ce que le champ d’accélération gravitationnelle puisse être considéré comme uniforme (g = 9,81 m/s2).
-
Physique
Loi de Gauss : distribution de charge continue
Généralisation de la loi de Gauss du champ électrique pour des distributions de charge continues. La somme discrète sur les charges intérieures à la surface (fermée) de Gauss est transformée en une intégrale de volume de la densité de charge dont le domaine d’intégration est le volume intérieur à la surface (fermée) de Gauss.
-
Mathématiques
Inversion matricielle
Sur base d’une interprétation géométrique de l’algèbre matriciel, nous établissons la formule générale de l’inversion matricielle.
-
Mathématiques
Propriétés du déterminant (1ère partie)
Trois propriétés de base du déterminant sont expliquées. Nous considérons les propriétés du déterminant en rapport avec les opérations de transposition matricielle et de permutation de lignes ou de colonne. De même, nous expliquons pourquoi une matrice dont deux lignes (colonnes) sont proportionnelles ont un déterminant nul.
-
Mathématiques
Formule du déterminant
Nous établissons la formule du déterminant d’une matrice en termes des cofacteurs des éléments de cette matrice.
-
Chimie
Solutions et concentration
Partant des mélanges, on cherchera à savoir ce qu’est une solution, comment on peut y définir la concentration d’un soluté et quelle est l’utilité de cette concentration.
