106 résultats pour “Ll”
-
Mathématiques
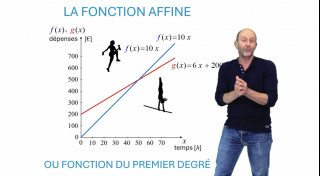
La Fonction affin
Suite à l’introduction de la fonction affine et de la fonction linéaire, nous proposons une analyse plus approfondie de la fonction affine avec pour but de familiariser l’élève avec la notion générale de fonction.
-
Mathématiques
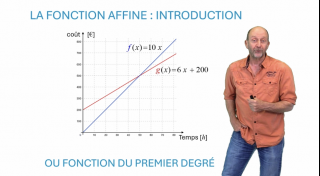
La Fonction affine, introduction
Nous introduisons la fonction affine dans un contexte appliqué à l’aide un problème de la vie de tous les jours.
-
Mathématiques
La Fonction, introduction
Nous présentons la notion mathématique de fonction dans un contexte appliqué qui conduit naturellement aux notions élémentaires de variable, de fonction d’une variable, de table de valeurs, de graphe d’une fonction, et de domaine de définition d’une fonction.
-
Mathématiques
Le théorème de l’angle inscrit : illustration
Nous illustrons le théorème de l’angle inscrit au travers du spectromètre à réseau concave de Henry Rowland
-
Mathématiques
Le théorème de l’angle au centre, illustration
Nous illustrons le théorème de l’angle au centre dans le contexte de la photographie et de la vision.
-
Mathématiques
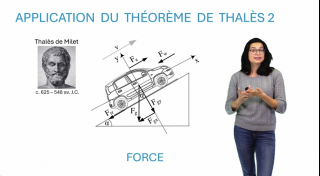
Application du théorème de Thalès 2 : force
Nous appliquons le théorème de Thalès à l’étude d’un système de forces simple.
-
Mathématiques
Comment Archimède a-t-il calculé le volume de la sphère ?
Nous décrivons la démarche utilisée par Archimède pour obtenir la formule qui donne le volume d’une sphère en fonction de son rayon.
-
Mathématiques
Volume de la sphère
A l’aide de la méthode de décomposition infinitésimale, nous établissons la formule qui donne le volume de la sphère en fonction de son rayon.
-
Mathématiques
La surface de la sphère
A l’aide de la méthode de décomposition infinitésimale, nous établissons la formule qui donne la surface de la sphère en fonction de son rayon.
-
Mathématiques
Décomposition infinitésimale et intégration
L’objectif de cette séquence est de faire comprendre le passage de la décomposition infinitésimale à l’opération mathématique d’intégration qui lui est indissociable. Cette séquence est très utile à l’élève qui n’est pas à l’aise avec l’interprétation de la notion d’intégrale.
