10 vidéos ayant le tag “gradient”
-
 Physique
Physique
Équations de Poisson et Laplace : illustration
Nous discutons de l’interprétation physique des équations de Laplace et de Poisson de façon à familiariser l’élève avec l’opérateur laplacien.
Nous montrons que l’équation de Laplace exprime une relation simple entre les dérivées secondes partielles par rapport aux trois coordonnées d’espace. A deux dimensions cette relation s’exprime en disant que les courbures des variations du potentiel dans deux directions orthogonales sont opposées. -
 Physique
Physique
Équations de Poisson et Laplace
Dérivation de l’équation de Poisson de l’électrostatique à partir de la loi de Gauss et de la notion de potentiel électrique. L’équation de Poisson est vue comme l’expression de la loi de Gauss en termes de potentiel électrique. Nous profitons de ce développement pour familiariser l’élève à la notion d’opérateur différentiel.
-
 Physique
Physique
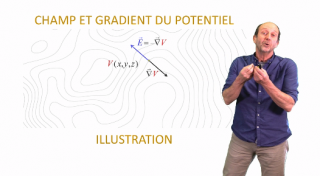
Champ et gradient du potentiel : illustration
À l’aide de quelques exemples, nous illustrons la formule donnant le champ électrique à partir du potentiel électrique.
-
 Physique
Physique
Champ et gradient du potentiel
Nous expliquons la procédure qui permet d’établir que le champ électrique est égal à l’opposé du gradient du potentiel électrique.
-
 Mathématiques
Mathématiques
Le gradient : exercice
Exercice résolu sur la notion de gradient dans le cas d’une fonction de deux variables.
-
 Mathématiques
Mathématiques
Le gradient : généralisation à 3 dimensions
Nous généralisons le concept de gradient en passant à l’étude des variations des fonctions de trois variables.
-
 Mathématiques
Mathématiques
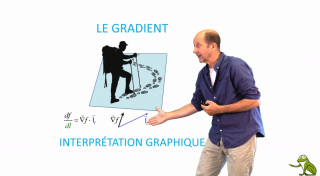
Le gradient : interprétation graphique
Nous proposons une astuce graphique permettant une interprétation plus aisée de la notion de gradient.
-
 Mathématiques
Mathématiques
Gradient et lignes de niveau
Nous démontrons que le champ vectoriel « gradient » d’une fonction de deux variables est en tout point perpendiculaire aux lignes de niveau de cette fonction.
-
 Mathématiques
Mathématiques
Le gradient : illustration
Illustration du concept mathématique de gradient au travers d’un problème simple d’optimisation.
-
 Mathématiques
Mathématiques
Le gradient, la dérivée directionnelle
A partir d’un problème simple d’optimisation nous introduisons la notion de gradient et de dérivée directionnelle.

