-
Physique
la force de Lorentz
Nous proposons de familiariser l’élève avec le concept de force de Lorentz au travers d’un travail d’interprétation physique. Nous abordons, en particulier le rôle de l’angle que fait la vitesse de la charge avec le champ magnétique et discutons les ordres de grandeurs très différents rencontrés en pratique pour la force de Laplace, d’une part, et la force de Lorentz, d’autre part.
-
Physique
De la force de Laplace à la force de Lorentz
Nous proposons l’étude de l’origine physique de la force magnétique de Laplace. Nous procédons pour cela à l’analyse mathématique de la notion d’élément de courant.
-
Physique
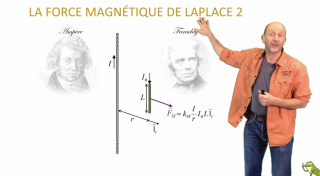
La force magnétique de Laplace 2
Nous étudions la force magnétique qui s’exerce sur un courant rectiligne plongé dans un champ magnétique uniforme dans la situation générale d’un angle quelconque entre le courant et le champ. Nous obtenons de cette manière la généralisation de la force dite de Laplace.
-
Physique
La force magnétique de Laplace 1
Nous analysons l’expression de la force magnétique qui agit sur un courant plongé dans un champ magnétique dans le cas particulier d’un courant de direction perpendiculaire au champ.
-
Physique
Pourquoi un champ de force pour le monopôle magnétique ?
Nous discutons des raisons pour lesquelles Faraday a conçu le champ magnétique comme étant un champ de force qui agit sur le monopôle magnétique alors que selon Ampère un tel monopôle n’existe pas.
-
Physique
Pourquoi le concept de champ ?
Nous discutons des raisons pour lesquelles Faraday a introduit le concept de champ dans le domaine de l’électromagnétisme.
-
Physique
Équations de Poisson et Laplace : illustration
Nous discutons de l’interprétation physique des équations de Laplace et de Poisson de façon à familiariser l’élève avec l’opérateur laplacien.
Nous montrons que l’équation de Laplace exprime une relation simple entre les dérivées secondes partielles par rapport aux trois coordonnées d’espace. A deux dimensions cette relation s’exprime en disant que les courbures des variations du potentiel dans deux directions orthogonales sont opposées. -
Physique
Équations de Poisson et Laplace
Dérivation de l’équation de Poisson de l’électrostatique à partir de la loi de Gauss et de la notion de potentiel électrique. L’équation de Poisson est vue comme l’expression de la loi de Gauss en termes de potentiel électrique. Nous profitons de ce développement pour familiariser l’élève à la notion d’opérateur différentiel.
-
Physique
Champ et gradient du potentiel : illustration
À l’aide de quelques exemples, nous illustrons la formule donnant le champ électrique à partir du potentiel électrique.
-
Physique
Champ et gradient du potentiel
Nous expliquons la procédure qui permet d’établir que le champ électrique est égal à l’opposé du gradient du potentiel électrique.
