-
Mathématiques
Dérivée d’une composée de fonctions - Introduction
La formule de la dérivée d’une composée de fonctions, capitale d’un point de vue calculatoire en analyse, est présentée de deux manières différentes, après avoir pris un certain temps à illustrer l’importance de la composition de fonctions.
-
Mathématiques
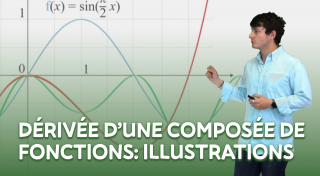
Dérivée d’une composée de fonctions - Illustrations
La formule de la dérivée d’une composée de fonctions est illustrée par de nombreux exemples divers.
-
Mathématiques
Liens entre fonctions trigonométriques et cyclométriques
Les liens de réciprocité entre les fonctions sin et arcsin, cos et arccos, tan et arctan sont analysés en détails.
-
Mathématiques
La dérivée seconde - Introduction
La dérivée seconde est introduite. Ses propriétés sont analysées sous différents angles : comme la dérivée de la dérivée première d’abord, ensuite sur base de sa définition analytique, puis sur base de constructions graphiques.
-
Mathématiques
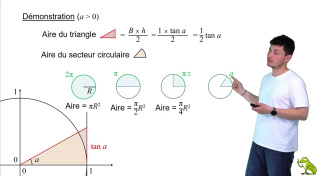
Approximation des petits angles
L’approximation des petits angles consiste à approximer le sin ou la tangente d’un arc proche de zéro par l’arc lui-même, et le cos correspondant à 1. Cette approximation est d’abord justifiée intuitivement, puis démontrée rigoureusement. Un lien avec l’analyse et des exemples d’application calculatoire sont présentés.
-
Mathématiques
Dérivées des fonctions harmoniques
Les dérivées des fonctions sin, cos et tan sont obtenues sur base de la définition de la dérivée d’une fonction. L’attelage écossais est présenté comme exemple d’application. Un lien avec l’approximation des petits angles est établi.
-
Mathématiques
La droite dans l’espace, équation cartésienne
Nous analysons et interprétons l’équation cartésienne de la droite dans l’espace à trois dimensions.
-
Mathématiques
La droite paramétrique, illustration
Nous illustrons l’équation paramétrique de la droite dans l’espace à l’aide d’un problème qui consiste à déterminer l’équation d’une droite passant par deux points donnés.
-
Mathématiques
La droite dans l’espace, équation paramétrique
Nous établissons l’équation paramétrique de la droite dans l’espace à trois dimension sur base de la connaissance d’un point appartenant à la droite et d’un vecteur parallèle à la droite (vecteur directeur).
-
Mathématiques
Le volume du cône (sans l’intégrale)
Nous proposons le calcul du volume du cône (sans recourir au concept mathématique d’intégrale) en l’assimilant au volume d’une pile de disques de petite épaisseur dont le rayon décroit linéairement avec la hauteur qu’ils occupent dans la pile.
