-
Physique
La loi d’Ohm, la résistance électrique
Nous expliquons l’origine physique de la loi d’Ohm sur base des notions de potentiel électrique et de courant électrique. L’approche consiste à calculer l’expression du courant électrique dans un matériau conducteur sur base de la notion de mobilité électronique.
-
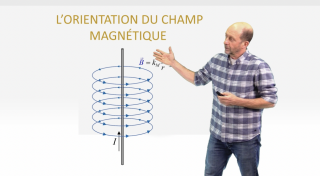Physique
Le potentiel électrique 2 : champ uniforme, illustration
L’objectif de cette séquence est de montrer que la notion de potentiel électrique peut, au travers de considérations énergétiques, être exploitée pour décrire le comportement des charges électriques.
-
Physique
Le potentiel électrique 1 : champ uniforme
Sur base d’un parallèle avec le potentiel gravitationnel nous présentons la notion physique de potentiel électrique. Nous expliquons brièvement, dans une perspective historique, comment et pourquoi cette notion est exploitée pour caractériser les piles électriques.
-
Physique
Méthode de Gauss 3 : le plan
Nous appliquons la loi de Gauss au calcul du champ électrique généré par une plaque rectangulaire uniformément chargée, y compris en des points intérieurs à la plaque elle-même.
-
Physique
Méthode de Gauss 2 : le cylindre
Nous appliquons la loi de Gauss au calcul du champ électrique généré par un cylindre uniformément chargé, y compris en des points intérieurs au cylindre.
-
Physique
Méthode de Gauss 1 : la sphère
Nous appliquons la loi de Gauss au calcul du champ électrique généré par une sphère uniformément chargée, y compris en des points intérieurs à la sphère.
-
Physique
Le potentiel : introduction II
Nous généralisons la notion de potentiel gravitationnel vue dans la première partie au cas d’un champ d’accélération gravitationnelle en 1/r2 (cf. loi de la gravitation universelle), ceci dans le but de préparer l’élève au potentiel électrique de la charge ponctuelle (potentiel coulombien).
-
Physique
Le potentiel : introduction I
Dans le but de préparer l’élève au concept de potentiel électrique, nous introduisons la notion de potentiel dans le contexte de la force gravitationnelle. Dans cette première partie nous ne considérons que des situations à petite échelle à la surface de la Terre de sorte à ce que le champ d’accélération gravitationnelle puisse être considéré comme uniforme (g = 9,81 m/s2).
-
Physique
Théorème d’Ostrogradski
Explication intuitive du théorème d’Ostrogradski (ou théorème de flux-divergence).
-
Physique
Loi de Gauss : forme locale
Nous dérivons la forme locale de la loi de Gauss à partir de sa forme intégrale. Nous introduisons pour cela la notion mathématique de divergence d’une fonction à valeur vectorielle.
