-
Mathématiques
La fonction arccos
La fonction arccos, sa définition, son graphe, son domaine et son image sont étudiés en détail à partir de la connaissance de la fonction arccos.
-
Mathématiques
La fonction arctan
La fonction arctan, sa définition, son graphe, son domaine et son image sont étudiés en détail.
-
Mathématiques
Liens entre fonctions trigonométriques et cyclométriques
Les liens de réciprocité entre les fonctions sin et arcsin, cos et arccos, tan et arctan sont analysés en détails.
-
Mathématiques
Dérivées des fonctions cyclométriques
Les dérivées des trois fonctions cyclométriques étudiées dans CliPeDia (arcsin, arccos, arctan) sont présentées.
-
Mathématiques
La dérivée seconde - Introduction
La dérivée seconde est introduite. Ses propriétés sont analysées sous différents angles : comme la dérivée de la dérivée première d’abord, ensuite sur base de sa définition analytique, puis sur base de constructions graphiques.
-
Mathématiques
La dérivée seconde – Applications
Le calcul de la dérivée seconde, définie comme la dérivée de la dérivée, est appliqué à quelques cas de fonctions.
-
Mathématiques
Transformations graphiques - I
Les translations, étirements et compressions à partir du graphe d’une fonction quelconque sont abordés dans cette capsule.
-
Mathématiques
Les formules de Simpson
Les formules de Simpson (somme vers produit et vice-versa, aussi appelées formules de linéarisation dans certains cas) sont obtenues très simplement sur base des formules des cos et sin de sommes d’angles. L’étude du battement entre deux ondes sonores est présenté comme exemple d’application de ces formules.
-
Mathématiques
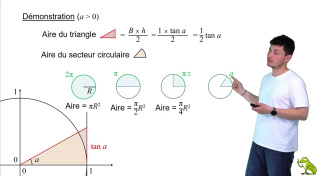
Approximation des petits angles
L’approximation des petits angles consiste à approximer le sin ou la tangente d’un arc proche de zéro par l’arc lui-même, et le cos correspondant à 1. Cette approximation est d’abord justifiée intuitivement, puis démontrée rigoureusement. Un lien avec l’analyse et des exemples d’application calculatoire sont présentés.
-
Mathématiques
Dérivées des fonctions harmoniques
Les dérivées des fonctions sin, cos et tan sont obtenues sur base de la définition de la dérivée d’une fonction. L’attelage écossais est présenté comme exemple d’application. Un lien avec l’approximation des petits angles est établi.
