-
 Mathématiques
Mathématiques
Les fonctions réciproques
La notion de réciproque d’une fonction et le lien graphique entre une fonction et sa réciproque sont présentés. Les notions de bijection et de restriction sur un intervalle du domaine sont abordées, et les incohérences potentielles illustrées par le biais de la fonction f(x) = x².
-
 Mathématiques
Mathématiques
Formule d'addition de la tangente
La formule de la tangente d’une somme d’angles est présentée, en commençant par le cas particulier de l’angle double. La tangente d’une différence d’angle est déduit de la formule de base. Des exemples sont présentés.
-
 Mathématiques
Mathématiques
Formules d'angles associés
Sur base de constructions géométriques dans le cercle trigonométrique ainsi que de vérifications algébriques, les relations qui existent entre les sinus, cosinus, et tangente d’un angle avec ses angles associés (opposé, supplémentaire et complémentaire) sont présentées.
-
 Mathématiques
Mathématiques
Le zéro et l’infini
Nous proposons une brève analyse historique des notions mathématiques de zéro et d’infini.
-
 Mathématiques
Mathématiques
La droite dans l’espace, équation cartésienne
Nous analysons et interprétons l’équation cartésienne de la droite dans l’espace à trois dimensions.
-
 Mathématiques
Mathématiques
La droite paramétrique, illustration
Nous illustrons l’équation paramétrique de la droite dans l’espace à l’aide d’un problème qui consiste à déterminer l’équation d’une droite passant par deux points donnés.
-
 Mathématiques
Mathématiques
La droite dans l’espace, équation paramétrique
Nous établissons l’équation paramétrique de la droite dans l’espace à trois dimension sur base de la connaissance d’un point appartenant à la droite et d’un vecteur parallèle à la droite (vecteur directeur).
-
 Physique
Physique
La résistance au roulement, 1ère partie
Nous proposons une analyse de l’origine physique de la résistance au roulement qui se manifeste sur un vélo en déplacement.
-
 Physique
Physique
La résistance au roulement, 2ème partie
Sur base du modèle physique développé dans la première partie, nous établissons une approche mathématique permettant d’appréhender la façon dont la résistance au roulement dépend de la largeur des pneus.
-
 Mathématiques
Mathématiques
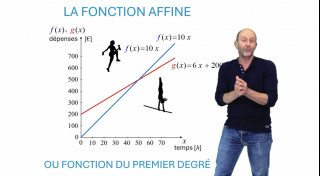
La Fonction affine
Suite à l’introduction de la fonction affine et de la fonction linéaire, nous proposons une analyse plus approfondie de la fonction affine avec pour but de familiariser l’élève avec la notion générale de fonction.

