-
 Mathématiques
Mathématiques
La Fonction linéaire
Sur base de la leçon d’introduction à la fonction affine, nous présentons la fonction linéaire comme un cas particulier de fonction affine correspondant à une ordonnée à l’origine nulle. La fonction linéaire représente donc une simple relation de proportionnalité entre la fonction et sa variable.
-
 Mathématiques
Mathématiques
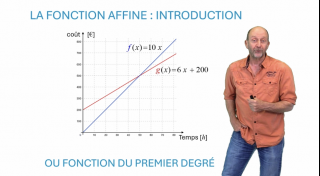
La Fonction affine, introduction
Nous introduisons la fonction affine dans un contexte appliqué à l’aide un problème de la vie de tous les jours.
-
 Mathématiques
Mathématiques
La Fonction, introduction
Nous présentons la notion mathématique de fonction dans un contexte appliqué qui conduit naturellement aux notions élémentaires de variable, de fonction d’une variable, de table de valeurs, de graphe d’une fonction, et de domaine de définition d’une fonction.
-
 Mathématiques
Mathématiques
Le volume du cône (sans l’intégrale)
Nous proposons le calcul du volume du cône (sans recourir au concept mathématique d’intégrale) en l’assimilant au volume d’une pile de disques de petite épaisseur dont le rayon décroit linéairement avec la hauteur qu’ils occupent dans la pile.
-
 Mathématiques
Mathématiques
La surface du cône
La surface latérale du cône est calculée à partir de la décomposition du cône en triangles isocèles de très petite largeur.
-
 Mathématiques
Mathématiques
Le théorème de l’angle inscrit : illustration
Nous illustrons le théorème de l’angle inscrit au travers du spectromètre à réseau concave de Henry Rowland
-
 Mathématiques
Mathématiques
Le théorème de l’angle inscrit
Nous énonçons et démontrons le théorème de l’angle inscrit qui dit que dans un cercle deux angles inscrits qui interceptent le même arc ont la même mesure.
-
 Mathématiques
Mathématiques
Mesure, dimension, unité
Nous proposons une réflexion sur les notions scientifiques de base que représentent les concepts de mesure, de dimension et d’unité.
-
 Mathématiques
Mathématiques
Le théorème de l’angle au centre, illustration
Nous illustrons le théorème de l’angle au centre dans le contexte de la photographie et de la vision.
-
 Mathématiques
Mathématiques
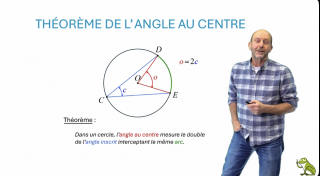
Le théorème de l’angle au centre
Nous énonçons et démontrons le théorème de l’angle au centre qui dit que l’angle au centre d’un cercle vaut le double de tout angle inscrit au cercle qui intercepte le même arc.

