-
 Mathématiques
Mathématiques
Introduction à la mise en équation
Nous introduisons le concept de mise en équation au travers d’une petite histoire impliquant une commerçante au prise avec un ajustement de marge bénéficiaire.
-
 Mathématiques
Mathématiques
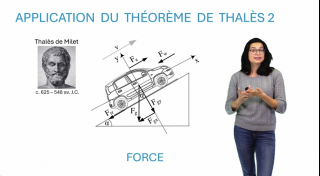
Application du théorème de Thalès 2 : force
Nous appliquons le théorème de Thalès à l’étude d’un système de forces simple.
-
 Mathématiques
Mathématiques
Le théorème de la médiane pour le triangle rectangle
Nous énonçons et démontrons le théorème de la médiane pour le triangle rectangle. Nous énonçons également deux corollaires de ce théorème ainsi que le théorème réciproque.
-
 Mathématiques
Mathématiques
Comment Archimède a-t-il calculé le volume de la sphère ?
Nous décrivons la démarche utilisée par Archimède pour obtenir la formule qui donne le volume d’une sphère en fonction de son rayon.
-
 Mathématiques
Mathématiques
Volume de la sphère
A l’aide de la méthode de décomposition infinitésimale, nous établissons la formule qui donne le volume de la sphère en fonction de son rayon.
-
 Mathématiques
Mathématiques
La surface de la sphère
A l’aide de la méthode de décomposition infinitésimale, nous établissons la formule qui donne la surface de la sphère en fonction de son rayon.
-
 Mathématiques
Mathématiques
Décomposition infinitésimale et intégration
L’objectif de cette séquence est de faire comprendre le passage de la décomposition infinitésimale à l’opération mathématique d’intégration qui lui est indissociable. Cette séquence est très utile à l’élève qui n’est pas à l’aise avec l’interprétation de la notion d’intégrale.
-
 Mathématiques
Mathématiques
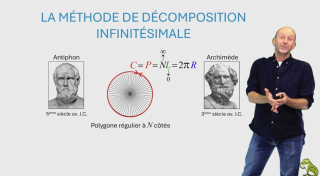
La méthode de décomposition infinitésimale
Afin de familiariser l’élève avec la méthode de décomposition infinitésimale qui sous-tend le calcul intégral, nous proposons une analyse de la méthode mise en œuvre par Archimède pour calculer l’aire du cercle.
-
 Mathématiques
Mathématiques
Introduction au calcul infinitésimal
Nous proposons une introduction historique au calcul infinitésimal en nous basant sur la méthode exploitée par Archimède pour calculer la circonférence du cercle (et le nombre pi). Cette méthode proposée par Antiphon au 5ème siècle avant J.C. consiste en effet à réaliser une décomposition infinitésimale du cercle en segments de droites.
-
 Mathématiques
Mathématiques
L’aire du cercle
Nous présentons la technique qui a permis à Archimède de découvrir la formule de l’aire du cercle à partir de la formule de la circonférence du cercle.

